🌾kiayun手机版登录云手机版登录(官方)网站/网页版2025最新版本V4.20

物联网概述 涉及多重，范围广泛的物联网，以传感器、网络以及数据处理技术，把各类物体连至互联网，达成智能管理与控制，其应用领域从智能家居延伸至工业自动化，从健康监测拓展到智慧城市，持续改变着我们的生活与工作方式，它也被简称为IoT，全称为Internet of Things 。 1.1 物联网的定义 物联网是...

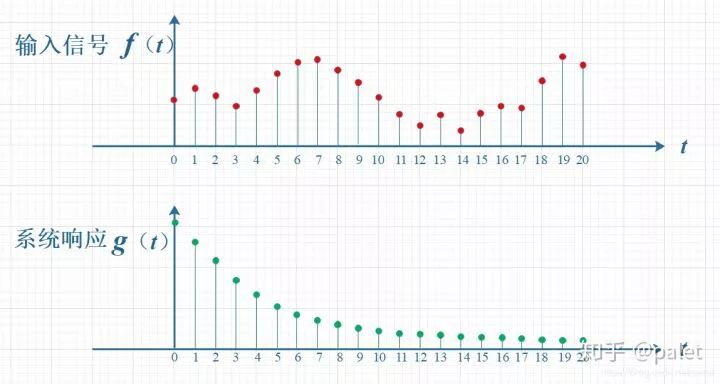
点击上方“小白学视觉”，选择加"星标"或“置顶” 重磅干货，第一时间送达 1、对卷积的困惑 曾经在很早之前就学习过卷积这个概念，不过一直都没弄明白，教科书通常会给出定义，会给出众多性质，还会运用实例跟图形来进行解释，然而到底为何要如此设计，如此计算，其背后的意义是什么，常常说得不清楚；作为一个有学物理背景出身...

卷积属于一种基本的数学运算，它于信号处理里被广泛运用，它于图像处理之处被广泛采用，它于神经网络范畴被广泛利用。 如下方式可对卷积的原理予以描述：设有两个函数f(x)，还设有函数g(x)，它们于定义域内的乘积积分被表示成： 在这里，*代表卷积操作，g(x - τ)指的是函数g(x)朝着右边平移τ个单位，即g(...

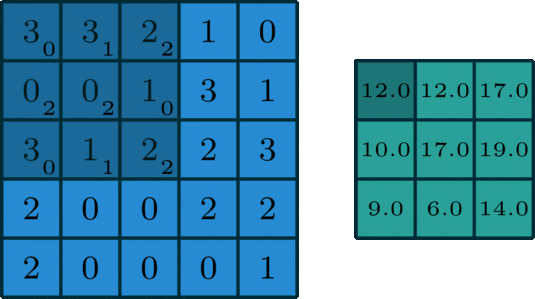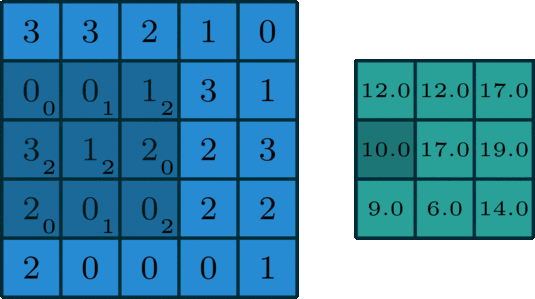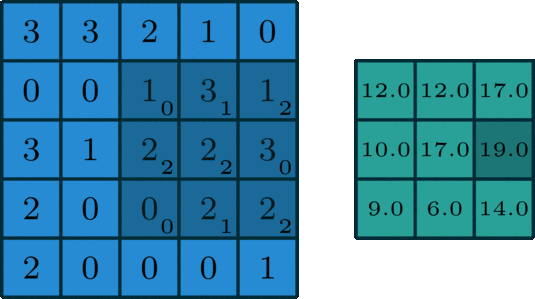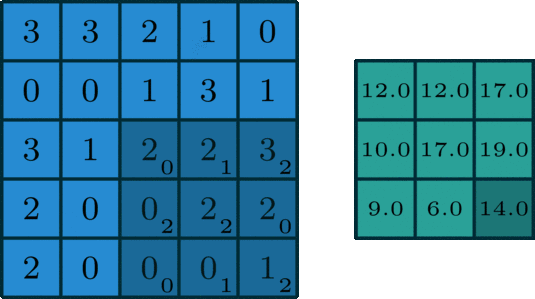
一、卷积是啥卷积（Convolution） 有一种数学运算，它存在于信号处理以及图像处理当中，此运算在计算机视觉、深度学习等诸多领域有着广泛应用。卷积操作是这样进行的，它会滑动一个滤波器，这个滤波器也被称作卷积核或者卷积滤波器，在输入数据上滑动，这部分输入数据比如有图像，通过这样的滑动处理后，最终生成一个特征...

针对斐波那契数列在股票市场里的适用情况，我们谈谈什么是斐波那契数列，它又被称作黄金分割数列，所指的是这样的一个数列，先是1，紧接着是1开·云体育app下载安装，然后是2，再然后是3，之后是5，接着是8，再之后是13，随后是21，。 数学、化学以及物理等领域，该系列有着广泛应用，常用于股票期货。《期货市场技术分...

浅谈菲波纳契数列的内涵和应用价值 99数学本四班 莫少勇指导教师 孙丽英 论文摘要开头，本文起始于菲波那契数列，借由对其数学内涵予以深究，以及对其在现实生活里应用的探寻，来提升学生针对数学的欣赏水平，初步构建起数学建模的思维理念kia云手机版登录，因而提升运用数学知识剖析实际问题的能力。 关键词 Fi...

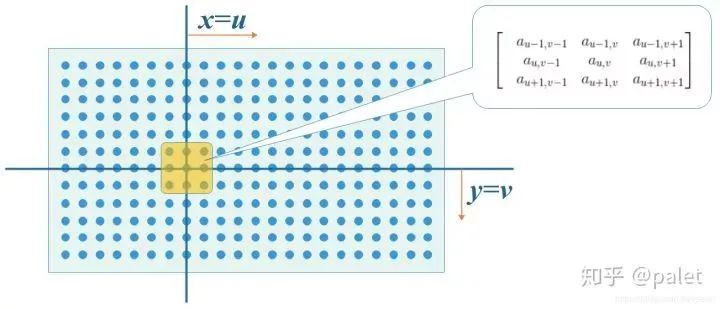
把卷积，也就是Convolution，说成是一种极其复杂的数学处之手段不算过，它的应用范围特别广泛，像信号处理时会用到它，图像处理领域也会用到它，机器学习范畴也缺不了它，神经网络这个领域同样用得上它。它存在着一维的定义以及应用这方面情况，还有二维、三维的定义以及应用这方面情形。在这儿，我们仅仅是对一维意义下的...

用于将两个函数或信号合并成一个新的函数或信号，以表示其中一个函数怎样去修改另一个函数的一种数学运算，是卷积操作，它在数学、信号处理、图像处理以及深度学习领域都存有广泛运用。于各种不同领域之中，卷积操作具体实现以及用途也许会存在差异，可是其基本数学原理却是相通的。 定义和数学表达 数学里，两个实数函数 f 与...

怎么去解释卷积这个名词呢，“卷”到底是什么含义呢，以及“积”又有着怎样的意思呢 ？ 卷积之中的“卷”，所指的乃是函数的翻转，即从g(t)转变为g(-t)的这一过程，与此同时，“卷”还存在着滑动的那种意味在其中，此乃吸取了网友李文清的建议。要是将卷积翻译为“褶积”，那么这个“褶”字便仅仅只有翻转的含义了。 卷积...

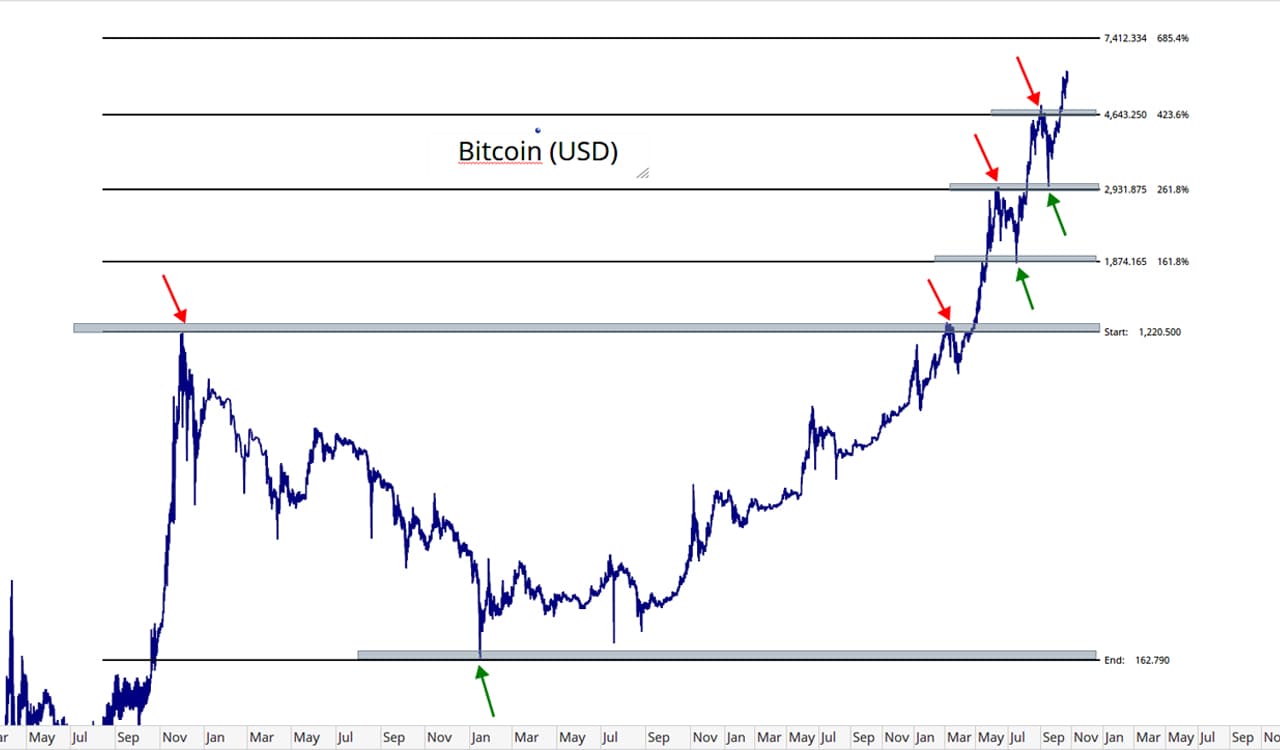
斐波那契属于一种价格指标，它在其他金融市场也有着广泛应用。斐波那契是什么？又该如何使用它？这些问题的答案相当重要，原因是众多投资者对于如何运用斐波那契指标并不清楚。 这个数列叫斐波那契数列，它因意大利 mathematician 莱昂纳多·斐波那契的出名得有这名称， discovery 的时期是那世纪（13...