🌾kiayun手机版登录云手机版登录(官方)网站/网页版2025最新版本V4.20

初二上册第一单元的核心内容是勾股定理，同学们通过学习已经掌握了运用勾股定理解决直角三角形问题的技巧。然而，在这一章节的学习过程中，大家可能会遇到一些特定题型kaiyun官方网站登录入口，那就是运用勾股定理解决图形折叠的问题，这类问题通常包括三角形的折叠和四边形的折叠等。今天，我们将一起探讨这类题型有哪些常见的...

3D打印，照亮未来 3D打印技术普遍通过数字技术与材料打印机相结合来实现，尽管这项技术问世已久，但始终有新的应用不断涌现。随着其成本降低和普及度的提高，3D打印设备正逐渐成为现代社会不可或缺的产品。在医疗、航天、设计以及运输等多个领域，这些设备已经带来了深刻的变革。无论是用于为医疗患者进行生物打印，还是用于打...

勾股定理：数学之美在生活中的无尽奇妙 勾股定理开yun体育app官网网页登录入口，这一古老而神奇的数学规律，不仅局限于数学课本的乏味章节，它更是一种充满活力的思考方式，渗透在我们日常生活的点点滴滴。它通过三角形的简洁形态，揭示了数学的美丽，同时也蕴含着无穷的实用价值。让我们共同深入挖掘，领略数学的神奇魅力吧！...

随着科技的迅猛进步，往昔仅限于科幻小说的奇幻构想，现已悄无声息地融入了我们的日常。那些令人叹为观止的尖端科技产品，正以出人意料的方式，改变着我们的生活方式，将原本复杂的日常琐事变得既便捷又充满乐趣。现在，就让我为大家一一揭晓那些能够彻底革新生活的神奇黑科技产品。 智能烹饪机：厨房小白的逆袭神器 烹饪技艺不佳...

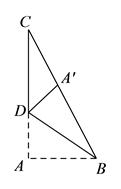
中考中，折叠问题既是热门也是难点，它常常与动点问题相互关联。这类问题的设定往往涉及将特定图形按照特定条件进行折叠，解答时需分析折叠前后的图形变化，并利用轴对称特性、勾股定理等知识来求解。 这类问题构思独特，变化多端，要妥善解决它们，不仅需要运用轴对称图形的特性来绘制所需图形，而且还需巧妙地运用各种数学模型与解...

纳米技术在日常生活中的应用 王老师为四年级的孩子们特别设计了《纳米技术就在我们身边》第七课的写作示例，以便他们能同步进行相关练习。若我有机会运用纳米技术，我打算探索其在日常生活的多个领域的应用。 纳米雨伞 纳米雨伞的制造中，其骨架部分巧妙地加入了纳米材料层，这样的设计使得伞在展开时仅需一根伞柄和一张伞面，而在...

如今，我们被数据包围，同时，又常常被数据欺骗。 我们怎样借助统计学来辅助我们做出正确的选择与判断。不要被依据历史数据统计出的模型迷惑，历史数据无法代表未来趋势kaiyun官方网站登录入口，通常历史上发生的事情都是随机事件，对未来发展毫无参考价值，不要被历史数据和模型误导。眼见不一定真实，图像也会歪曲数据，要小...

这份文档详细记录了在统计学实验中运用SAS软件进行数据处理的成果。其中，重点阐述了三种t检验技术：分别是针对单个样本的单样本t检验、针对成对数据的配对t检验，以及针对两组独立样本的成组设计两独立样本均数的t检验。单样本t检验的实验背景如下：已知健康人群的乙酰胆碱酯酶平均水平为1.44mmol/Lkaiyun全...

南都报道，记者王睦广指出开元棋官方正版下载，全国众多地区纷纷投身于智能传感器这一新兴生产力领域的竞争。特别是在深圳光明区，智能传感器产业已壮大成为百亿级别的产业集群，并成为光明区“3+3+1”产业集群中的关键一环。 近期，光明科技金融大厦成功举办了光明科学城知识产权交流会以及“创享汇”产业创新沙龙第五期活动。...

在日常生活中，我们常会遇到与统计学相关的案例，比如，股市的走势能否被预测？又比如，“吸烟会导致癌症”这样的结论是如何得出的？其可信度如何？为何需要进行新药的临床试验？为何民意调查仅通过收集一千至两千人的观点开yun体育app官网网页登录入口，便能揭示广大民众对事件的看法？这些调查结果是否可靠？（如候选人支持率...